Mathematik

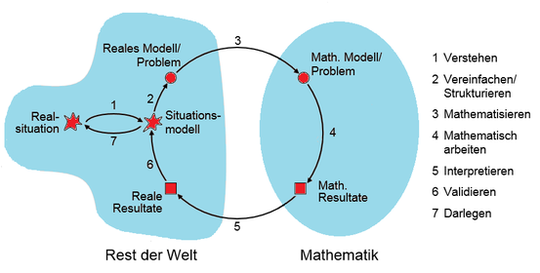
Modellierungskreislauf nach Blum/Leiß, Quelle: Schulministerium NRW

Die Mathematik ist kein Selbstzweck, sondern eine Dis­ziplin, die in vielen Bereichen der Wirtschaft, der Technik und der Naturwissenschaften von großer praktischer Be­deutung ist.
Mit Hilfe mathe­matischer Modelle auf der Basis von Funktionen und Gleichungs­systemen lassen sich Frage­stellungen des je­weiligen An­wendungs­gebietes untersuchen und damit plan- und be­rechenbar machen. Dabei wird von einer realen Situation abstrahiert, mathematisiert, interpretiert und argumentiert (siehe obiges Ablauf-/Phasenschema).
Das Spektrum solcher Modelle reicht von exakt bestimmbaren Zu­sammen­hängen bis hin zu stark vereinfachten Sichten auf die Wirklichkeit mit Näherungslösungen als Ergebnis.
Neben dem Erwerb des notwendigen mathematischen Hand­werkzeugs sollte daher das Entwickeln der Fähigkeit, dieses zielgerichtet für das Lösen von Anwendungsaufgaben einsetzen zu können, im Fokus des Unterrichts stehen.

Übungen & Anleitungen

Lineare Funktionen / Geraden

Arbeitsblatt Geradengleichung durch zwei Punkte
Lineare Funktion / Geradengleichung - Veranschaulichung
Übung Lineare Funktionen - Aufgabenblatt
Übung Lineare Funktionen - Lösungsblatt
Modellieren mit Linearen Funktionen - Aufgabenblatt
Arbeitsblatt Stückweise Lineare Funktion

Quadratische Funktionen / Parabeln

Grundtypen Quadratischer Funktionen - Übersicht
Arbeitsblatt Scheitelpunktform
pq-Formel & Quadratische Ergänzung - Übersicht / Beispiel
Übung Vier Wege zur Parabel - Aufgabenblatt
Übung Vier Wege zur Parabel - Lösungsblatt
Modellieren mit Quadratischen Funktionen - Aufgabenblatt
Modellieren mit Quadratischen Funktionen - Lösungsblatt
Arbeitsblatt Im Fokus: Parabolisches im Alltag (Sek II)

Geometrie / Trigonometrie / Winkelfunktionen

Arbeitsblatt Sonnige Aus-/Einsichten
Strahlensätze - Übersicht
Satz des Thales - Veranschaulichung / Beweisidee
Arbeitsblatt Tangente am Kreis
Satz des Pythagoras - Veranschaulichung
Übung Anwendungen Geometrie - Aufgabenblatt
Übung Anwendungen Geometrie - Lösungsblatt
Sinus, Cosinus und Tangens - Veranschaulichung am Einheitskreis
Übung Anwendungen Sinus-/Kosinussatz - Aufgabenblatt

Kurvendiskussion / Ganzrationale Funktionen

Arbeitsblatt Sekantensteigung / Mittlere Änderungsrate
Arbeitsblatt Tangentensteigung / Momentane Änderungsrate
Anleitung zur Kurvendiskussion
Übung Spektrum Kurvendiskussion - Aufgabenblatt
Übung Spektrum Kurvendiskussion - Lösungsblatt
Arbeitsblatt Trainingscamp Kurvendiskussion

Extremalwertberechnung

Arbeitsblatt Flächenoptimierung (Kaninchengatter)
Anleitung zur Extremalwertberechnung (mit Beispiel)
Übung Optimale Dosenform - Aufgabenblatt
Übung Optimale Dosenform - Lösungsblatt

Integralrechnung

Übung Kettenregel / Lineare Substitution - Aufgabenblatt
Übung Kettenregel / Lineare Substitution - Lösungsblatt
Übung A Abschnittsweise Integration - Aufgabenblatt
Übung B Produktregel / Fläche / Bilanz - Aufgabenblatt
Übungen A/B - Lösungsblatt
Übung 1 Fläche zwischen Graphen - Aufgabenblatt
Übung 1 Fläche zwischen Graphen - Lösungsblatt
Übung 2 Fläche zwischen Graphen - Aufgabenblatt
Übung 2 Fläche zwischen Graphen - Lösungsblatt

Analytische Geometrie

Gerade in Parameterform - Veranschaulichung
Ebene in Parameterform - Veranschaulichung
Ebene in Koordinatenform - VeranschaulichungNeu
Modellieren mit Vektoren / Geraden - Aufgabenblatt
Übung Grundlagen (GK/LK) - Aufgabenblatt
Übung Grundlagen (GK/LK) - Lösungsblatt
Übung Grundlagen (GK/LK) - Veranschaulichung

Abiturvorbereitung

Zur Vorbereitung auf das Zentralabitur ist es sinnvoll, sich neben dem selbstverständlich erforderlichen selbständigen Üben und Wiederholen des Unterrichtsstoffes mit Hilfe des in der Qualifikationsphase ver­wende­ten Lehrbuches auch mit den Vorgaben des Schulministeriums für das aktuelle Schuljahr sowie den Prüfungsaufgaben der vorhergehenden Jahre auseinanderzusetzen. Ziel bei letzterem sollte sein, nicht nur mit fachlichen Aspekten, sondern auch mit der Formulierung von Aufgaben­stellungen vertraut zu werden.

Die Vorgaben / Schwerpunktsetzung und auch die Aufgaben inklusive
der erwarteten Lösungen können hierzu von den Seiten des Schul­ministeriums NRW für das Fach Mathematik heruntergeladen bzw. dort nachgelesen werden.

Für den Zugang zu den Aufgaben ist eine Anmeldung mit Schulnummer und Kennwort erforderlich. Diese Informationen bitte bei mir erfragen.

Nach dem Abitur...

Viele Studienanfänger, die sich für eine technische Fachrichtung ent­schieden haben, sind über­rascht, in wie vielen Bereichen neben den Pflicht­vorlesungen Mathematik diese auch an praktisch orientierten Fach­hochschulen eine zentrale Rolle spielt und mit welcher Geschwindigkeit der Übergang von der Schul- in die Hochschulmathematik erfolgt.
Dies ist ein häufiger Stolperstein für ein erfolgreiches Absolvieren der ersten Semester.

Um den Einstieg zu erleichtern ist es daher eine gute Idee, die Zeit zwischen Abitur und Semesterstart für den Abbau möglicher Hürden zu nutzen (nach einer an­ge­messenen Erholungspause, selbstverständlich!).

Ein empfehlens­wertes Buch hierzu, das basierend auf Erfahrungen mit Erstsemestervorlesungen speziell für diesen Zweck von den Professoren D. Fröhling (West­fälische Hochschule Gelsenkirchen) und S. Kessel (TU Dortmund) konzipiert wurde, trägt den bezeichnenden Titel

   "NOTWENDIG und zunächst HINREICHEND".

Es ist 2009 im Shaker-Verlag erschienen (ISBN 978-3- 8322-8684-2) und für ein Selbststudium ausgelegt.

Nahezu alle Universitäten bieten auch einen mathematischen Vorkurs an. Auch hier ist es empfehlenswert, daran teilzunehmen oder sich zumindest das entsprechende Skript für ein Selbststudium zu beschaffen.

Wer sich zunächst nur orientieren und einen Blick in die genannten Materialien werfen möchte, kann sich beides auch bei mir ausleihen!

Tutorials zum GTR TI-nspire cx

Tutorials zum Grafiktaschenrechner TI-nspire cx. Natürlich kann man auch das Handbuch lesen, aber diese Video-Tutorials auf YouTube sind wirklich anschaulich.

Grundlegendes
 Grundlegende Bedienung des Scratchpad.
Grad-/Bogenmaß
 Trigonometrische Funktionen einstellen.
Nullstellen
 Nullstellen einer Funktion numerisch bestimmen.
Extremwerte
 Extremwerte einer Funktion numerisch bestimmen.
Gleichungssystem
 Lineare Gleichungssysteme lösen.
Integral
 Numerische Integrale berechnen.
Press-To-Test
 Den Press-To-Test-Modus deaktivieren.

Übungsmaterialien

Mathematikseiten gibt es zahlreich im Internet. Die Materialien auf der folgenden (subjektiven) Auswahl von Seiten haben sich bewährt und können einen Beitrag zum besseren Mathematikverständnis / Lernerfolg leisten.

www.selbstlernmaterial.de Umfangreiches, gut aufbereitetes und struk­turiertes Selbstlernmaterial zum Üben und Auffrischen, von Thomas Unkelbach.
www.strobl-f.de Grundwissen und Übungsaufgaben Mathe­matik bis zum Abitur, kompakt und über­sicht­lich, von Dr. Franz Strobl.
www.mathematik.de Die Seite der Deutschen Mathematiker-Vereinigung. Sie bietet ein vielfältiges Angebot, für Schüler/innen ist vor allem der "Erste Hilfe"-Bereich interessant.

 

Startseite Impressum © Klaus Milzner 2017